LLM
Christophe Cerisara
2024/2025
Attention
Content of today’s course
- Concepts of attention
- costs, KV cache
- Flash attention
- Implementation with tensors in Pytorch
cf. https://arxiv.org/pdf/2409.15790v1
Attention
- Intuition: transform word emb. using related context words
- See Lilian Weng blog
| Year | Authors | Contribution |
|---|---|---|
| 2014 | Graves et al | attention for Neural Turing Machines |
| 2014 | Bahdanau attention | application to NLP |
| 2015 | Luong attention | application to NLP |
| 2015 | Xu et al. | soft/global & hard/local |
| 2016 | Cheng, Dong and Lapata | self-att LSTMN |
| 2017 | Vaswani et al. | transformer, 120k citations |
KQV translation
\[\begin{equation} {\scriptsize{ \alpha_i = \frac {\exp(\text{score}(q,k_i))} {\sum_j \exp(\text{score}(q,k_j))} }} \end{equation}\] \[\begin{equation} {\scriptsize{ v' = \sum_i \alpha_i v_i }} \end{equation}\]
Similarity score
| name | score | ref |
|---|---|---|
| content-based | cosine\((q,k)\) | Graves14 |
| additive | \(v^T \tanh (W[q,k])\) | Bahdanau15 |
| location-based | \(\alpha = \text{softmax}(Wq)\) | Luong15 |
| general | \(q^T W k\) | Luong15 |
| dot-product | \(q^T k\) | Luong15 |
| scaled \(\cdot\) | \(\frac {q^t k} {\sqrt{d}}\) | Vaswani17 |
Scaled dot-product?
- Assume input E[k]=0 var(k)=1 \[var(xy) = (var(x)+E[x]^2)(var(y)+E[y]^2) - E[x]^2E[y]^2\]
- \(k\) and \(q\) independent: \(E[kq]=E[k]E[q]=0\) \[var(k_i q_i) = (var(k_i)+E[k_i]^2)(var(q_i)+E[q_i]^2) - E[k_i]^2E[q_i]^2 = 1\]
- Output variance: \[var\left(\sum_i k_iq_i\right) = \sum_i var(k_iq_i) = d\]
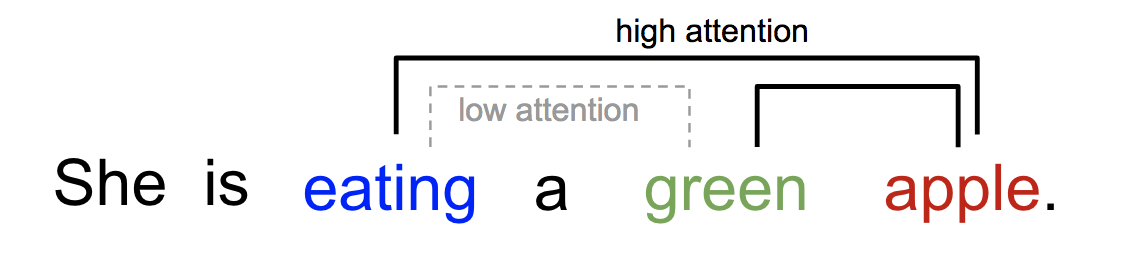
Self-attention
- Cheng 2016: use same sentence both for K and Q
- Often represented by a heat map over the words of the sentence

- Is attention interpretable? Does it enable explainability?
- No: cf. Why Attentions May Not Be Interpretable?
- Combinatorial shortcuts: attention carry extra info for next layers
- Other approaches: Integrated gradients, SHAP…
Matrix formulation
- arrange all keys \(k_i\) as a matrix \(K \in R^{N \times d}\)
- each vector \(k_i\) is a row of the matrix
- same for all queries \(q_i\) as \(Q \in R^{N \times d}\)
- \(A=\)sofmax\((QK^T)\)
- for each row, column, or globally?
- This matrix product outputs the new V = weighted sum of original V
- Beware of dimensions!
Self-attention with scaled dot-product:
\[V'=\text{softmax}\left(\frac {QK^T}{\sqrt{d}}\right)V\]
Cost
- The cost of \(QK^T\) is in \(O(n^2d)=O(n^2)\) operations
- But each of the \(n^2\) dot products can be computed in parallel, so we have \(O(1)\) sequential operations
- Transformers are well adapted to GPU!
- Compare to RNN: \(O(n)\) sequential operations
from https://slds-lmu.github.io/seminar_nlp_ss20/attention-and-self-attention-for-nlp.html
| Layer | Complexity | Seq. op |
|---|---|---|
| recurrent | \(O(nd^2)\) | \(O(n)\) |
| conv | \(O(knd^2)\) | \(O(1)\) |
| transformer | \(O(n^2d)\) | \(O(1)\) |
| sparse transf | \(O(n\sqrt{n})\) | \(O(1)\) |
| reformer | \(O(n\log n)\) | \(O(\log (n))\) |
| linformer | \(O(n)\) | \(O(1)\) |
| linear transf. | \(O(n)\) | \(O(1)\) |
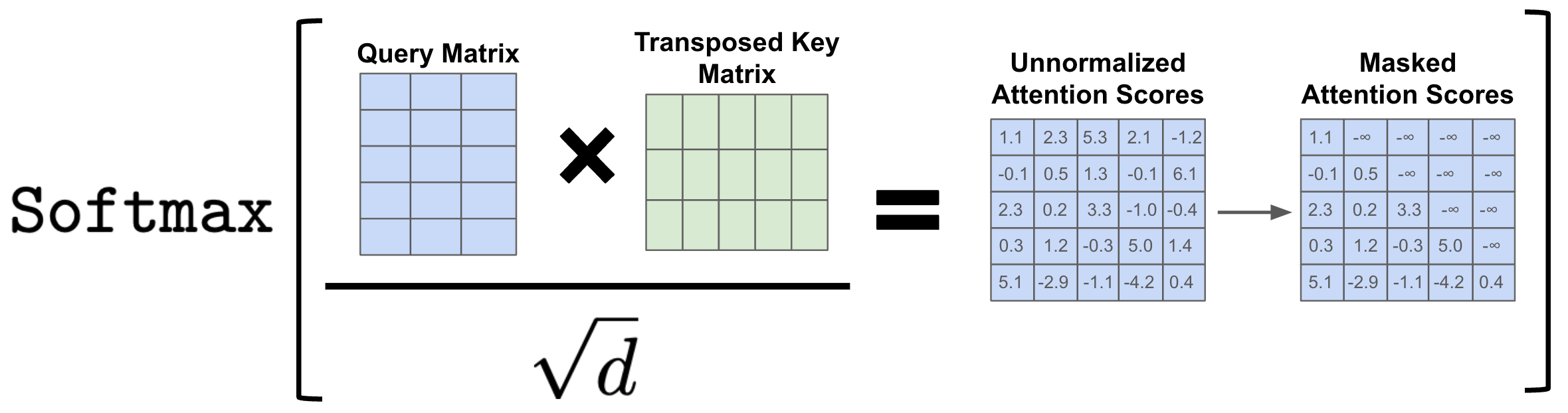
Training: Masked self-attention
- During training, the decoder is trained on sentence “The cat sat on the mat”:
- Step 1: loss = \(p("The"|\emptyset)\)
- Step 2: loss = \(p("cat"|"The")\)
- Step 3: loss = \(p("sat"|"The cat")\) …
- This is causal LM
- We could give the decoder 6 sub-sentences (“The”, “The cat”, …)
- But it’s more efficient to give it the full sentence, and train with a causal mask:
Inference: KV cache
\[Q,K \in R^{N\times d}\] \[QK^T \in R^{N\times N}\]
- So storing \(QK^T\) requires \(O(n^2)\) memory
- A decoder (GPT) generates each token with auto-regression:
- Each step recomputes self-att with \(N \leftarrow N+1\)
- We are recomputing each time the same attentions!
- Solution: save the already computed \(K\) and \(V\):
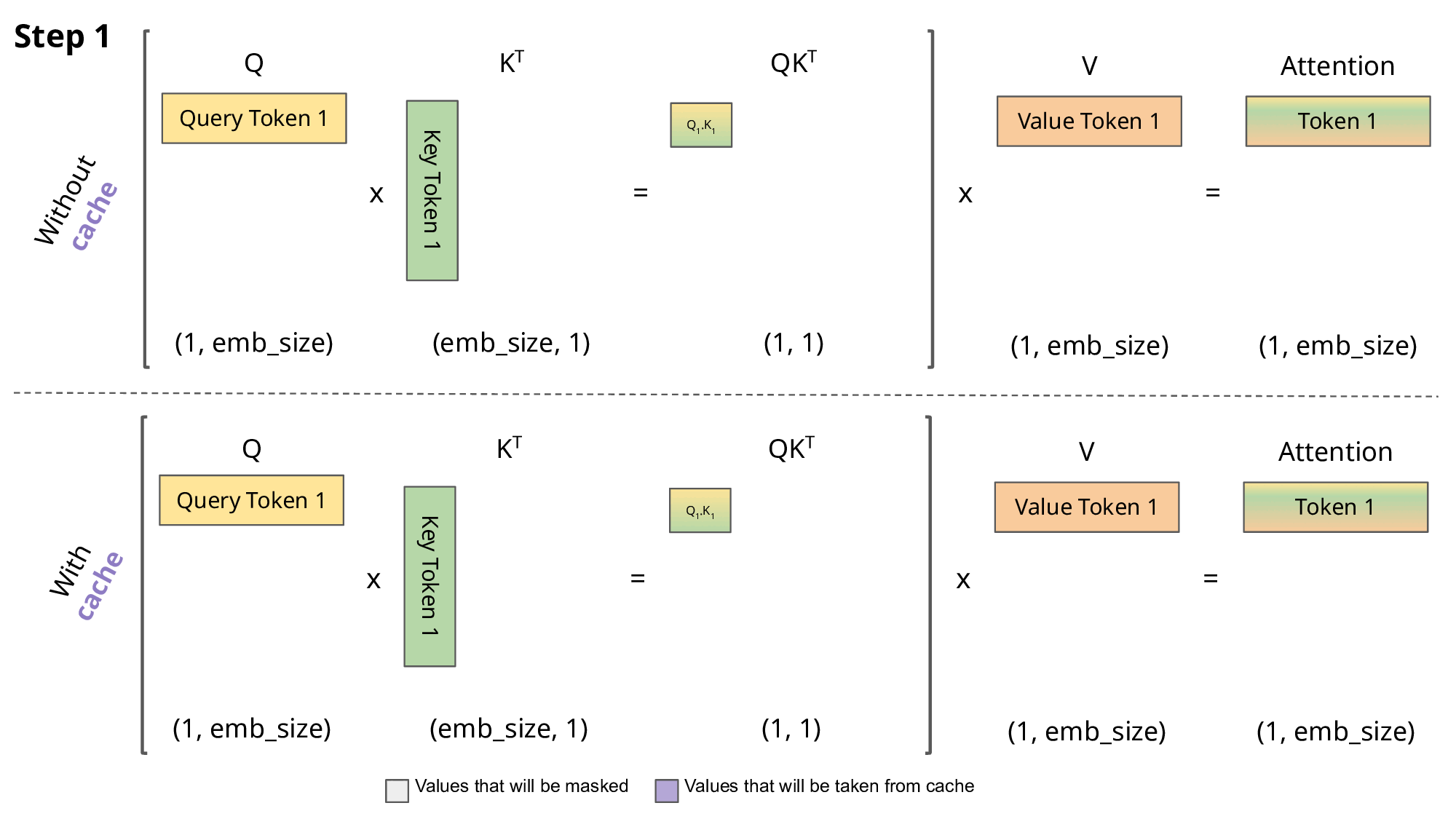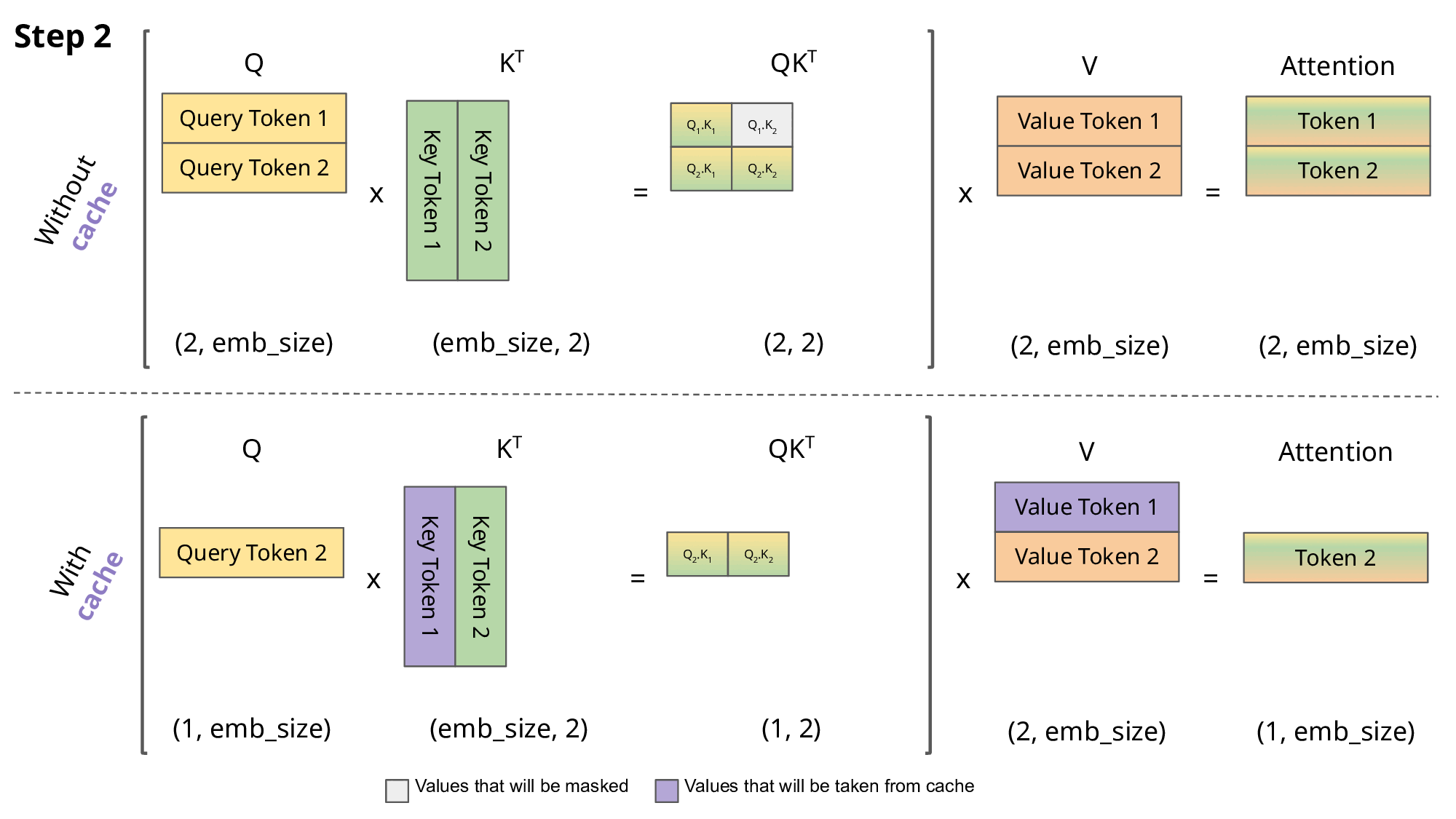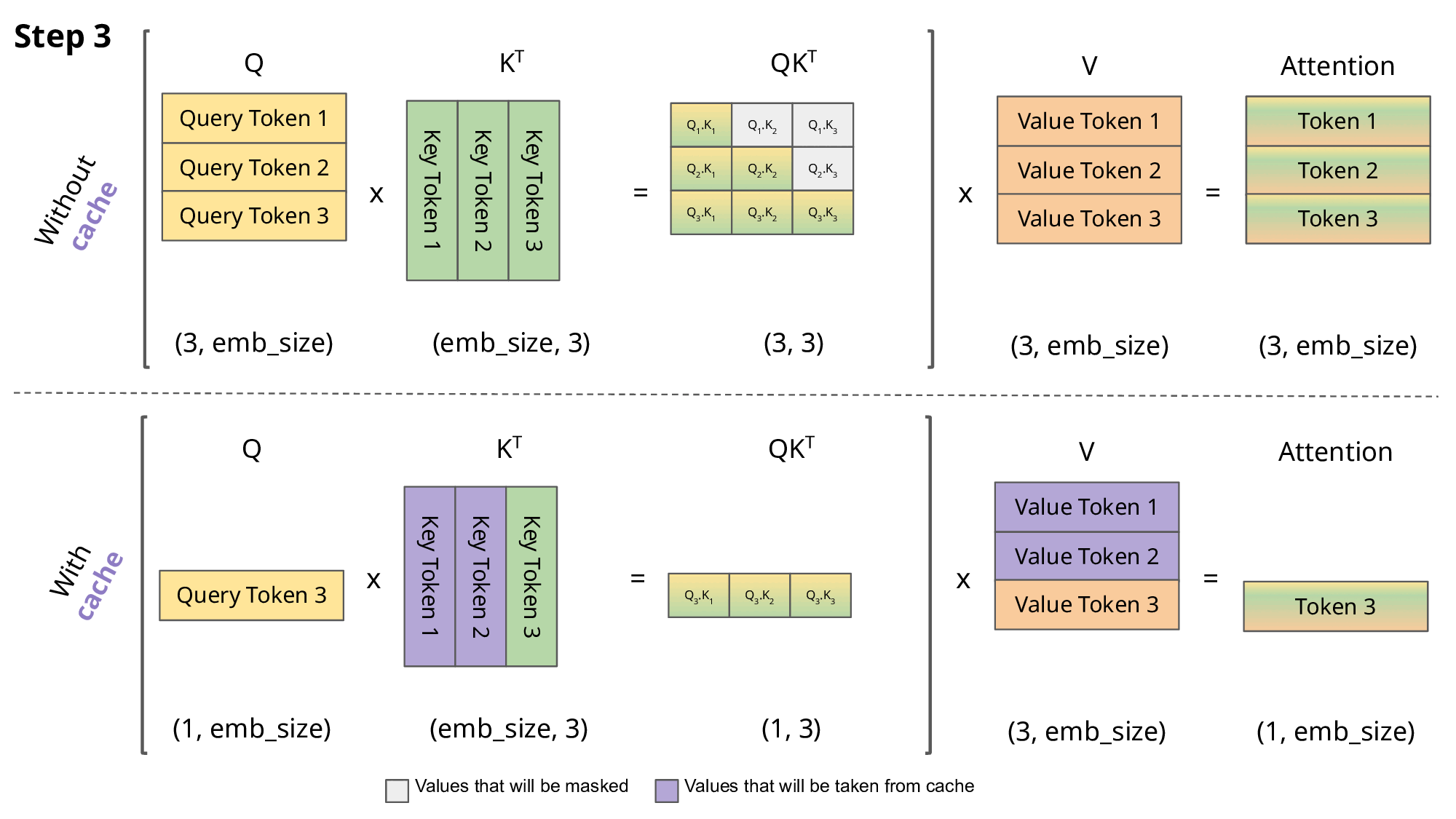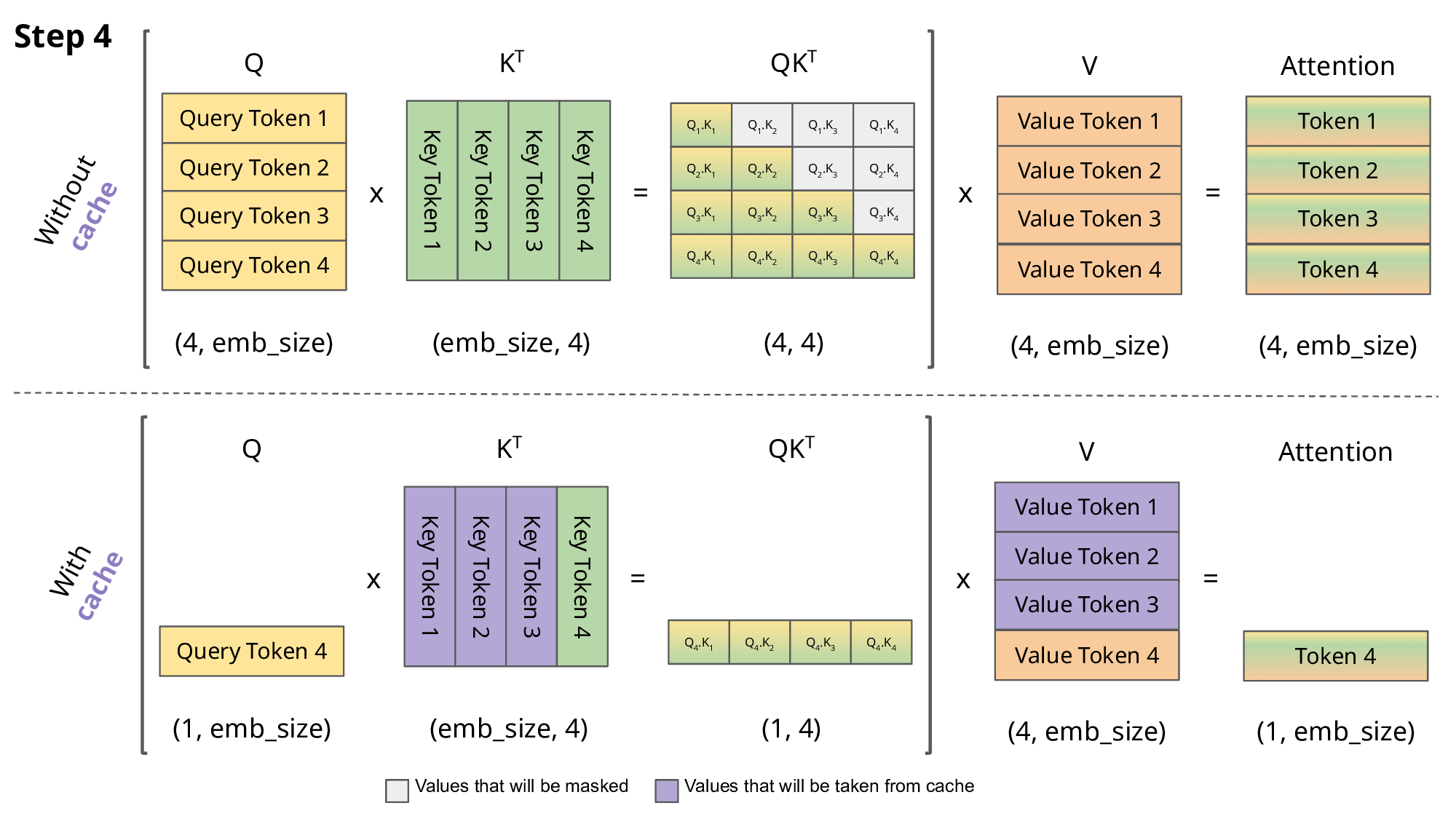
KV cache
- KV cache leads to
- faster matrix computations
- more memory to store cache
- New enhancements:
- KV cache quantization
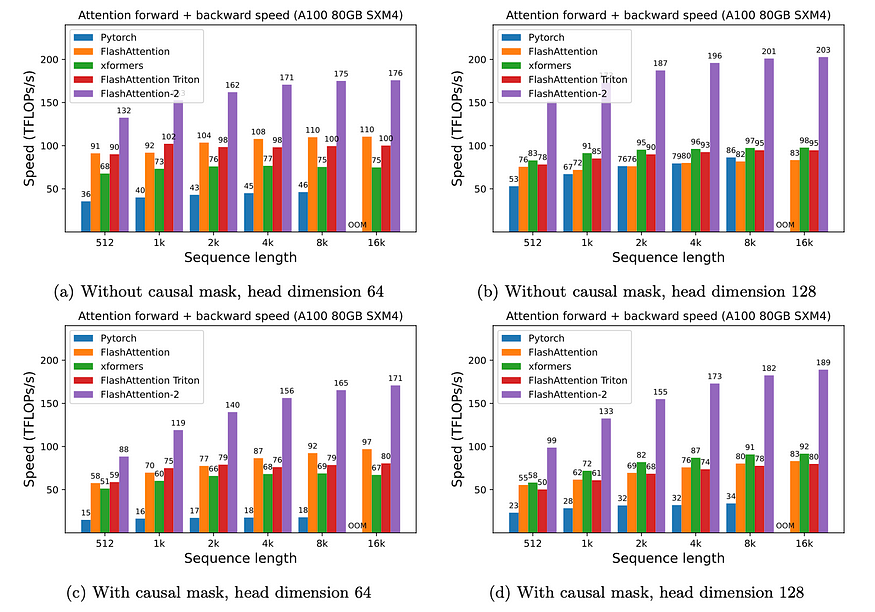
Flash Attention
- Bottleneck: memory I/O
- High Bandwidth Memory = large but slow
- GPU on-chip SRAM = small but fast
- Solution:
- fused kernels for self-att
- stay on-chip
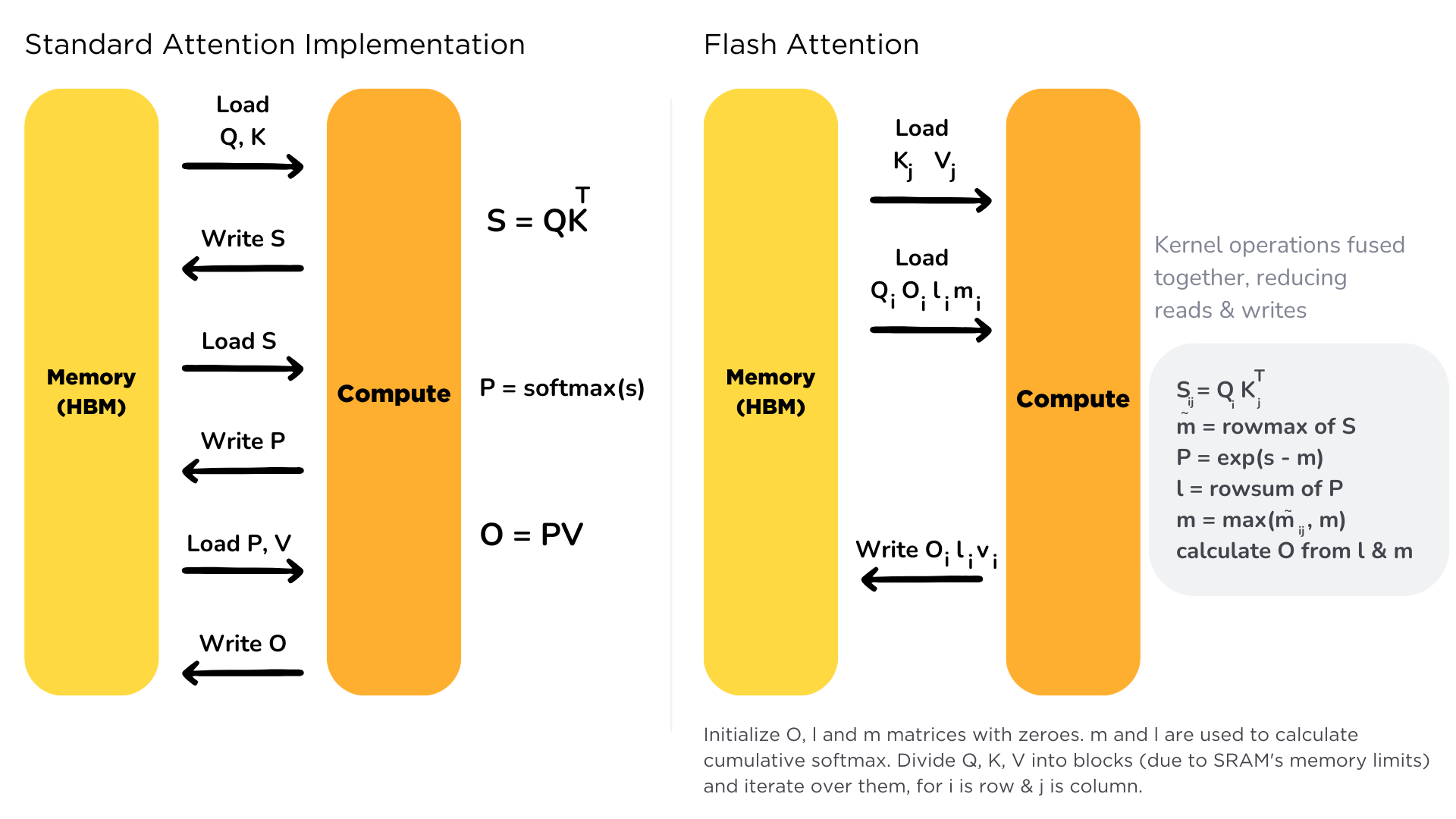
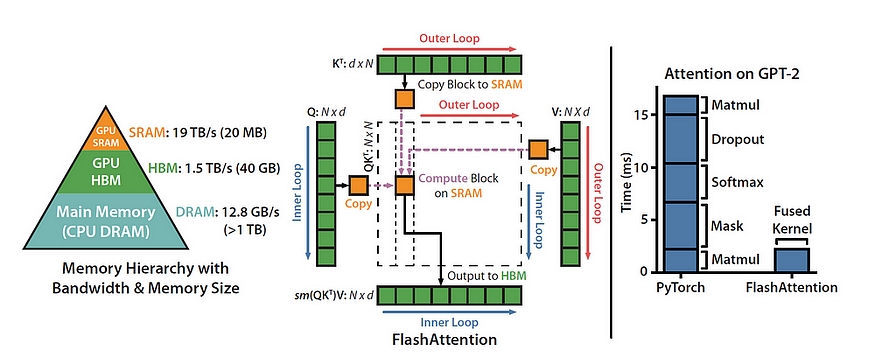
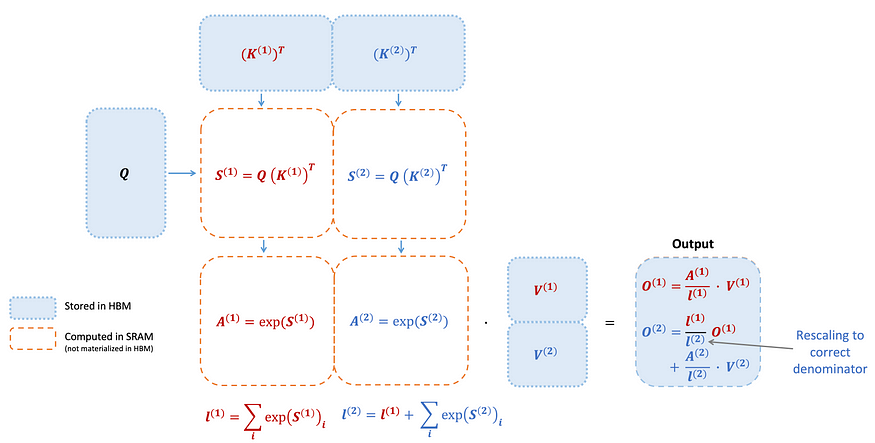
Flash Attention 2
- Divides and parallelizes the computation with the K and V matrices
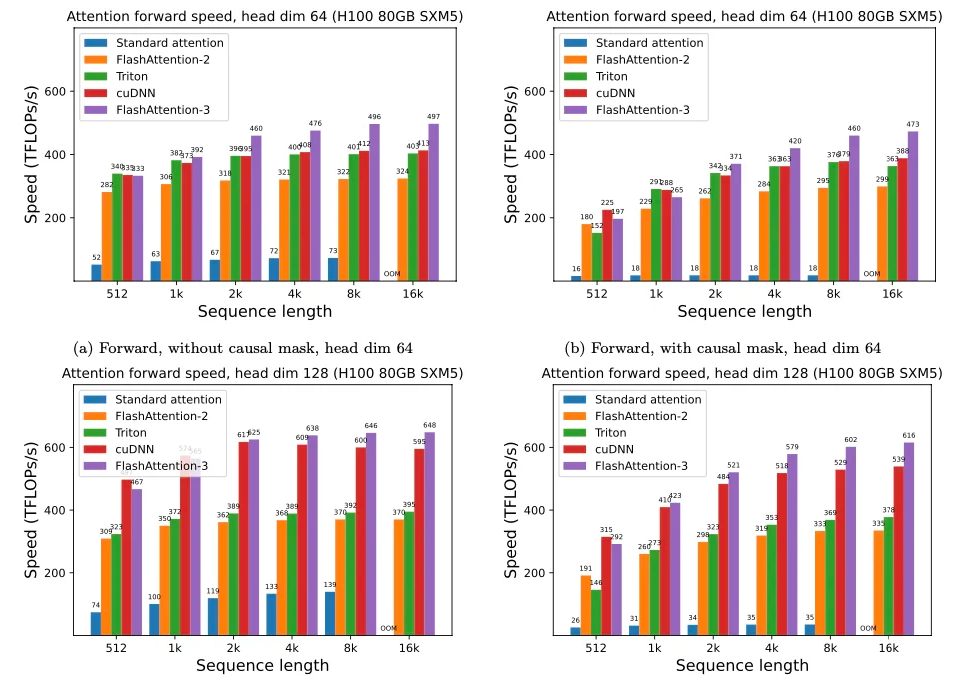
Flash Attention 3
- adapted to H100 GPU
- overlap warped matmuls and softmax
- FP8 “incoherent processing” (see QuiP) = multiplies the query and key with a random orthogonal matrix to “spread out” the outliers and reduce quantization error
Kernel optim on CPU
matmul on python: 0.042 GFLops
numpy (FORTRAN): 29 GFlops
reimplementation of numpy in C++: 47 GFlops
BLAS with multithreading: 85 GFlops
llama.cpp (focus matrix-vec): 233 GFlops
Intel’s MKL (closed source): 384 GFlops
OpenMP(512x512 matrix): 810 GFlops
exported in llamafile: 790 GFlops