LLM4ALL
LLM compression
cost reduction
Christophe Cerisara
CNRS, LORIA, Synalp team
Why do we want to compress LLMs?
Larger models are always better!

Bottom line: reduce inference costs
How to reduce compute at test time
- Algorithmic optimization: adv. KV-cache, FIRP, LAMPS, speculative decoding, FlashAttention3, …, CPU kernels:
| MatMul kernel | GFlops |
|---|---|
| matmul on python | 0.042 GFLops |
| numpy (FORTRAN) | 29 GFlops |
| reimplementation of numpy in C++ | 47 GFlops |
| BLAS with multithreading | 85 GFlops |
| llama.cpp (focus matrix-vec) | 233 GFlops |
| Intel’s MKL (closed source) | 384 GFlops |
| OpenMP(512x512 matrix) | 810 GFlops |
| exported in llamafile | 790 GFlops |
All these optimizations are complementary with compression!
How to reduce VRAM requirements
- Quantization: -75% !! But is quantization hitting ceiling?

(Digression) scaling laws
Scaling laws are the best thermometer/caliper of LLMs

Scaling laws govern training LLMs:

Scaling laws govern test-time compute reasoning:

Scaling laws govern in-context learning:

Compression better than quantization wrt scaling laws?

Reducing LLM size
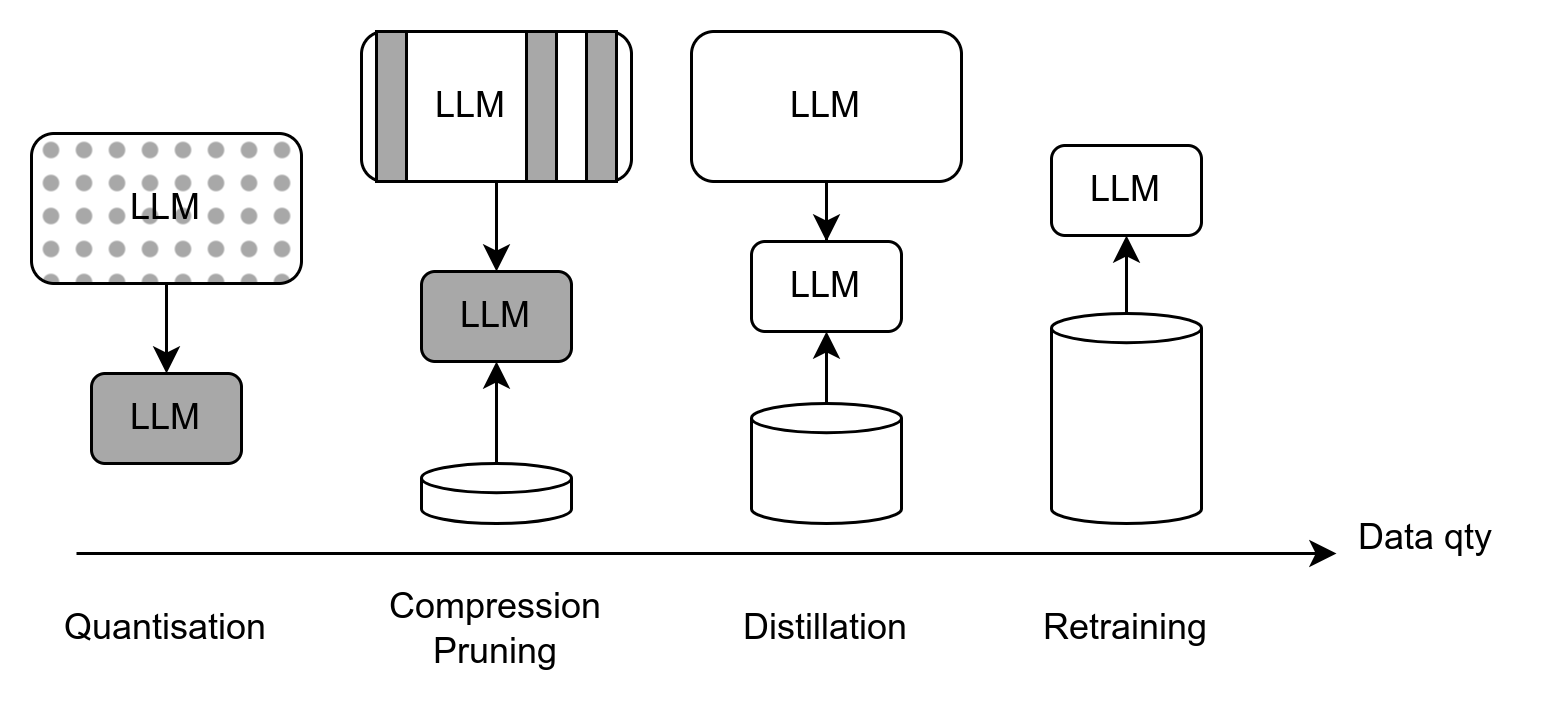
Compression: need calibration data

LLM Pruning: motivations
- Is there still any free space in LLM matrices? (parameter-efficiency)
- Otherwise, we may not need all this information at test time
- Pruning: remove “unused” or “superfluous” dimensions
- Metric to measure “emptiness”: matrix rank
LLM matrices are nearly full rank

But activations are low rank

- Principle: find a low-rank matrix that minimizes reconstruction error: \[\widehat{\Delta W} = \underset{{\Delta W}}{\mathrm{argmin}} \;\; \frac{1}{N}\sum\limits_{x \in \mathcal{D}}\|Wx - {\Delta Wx}\|_{F}\]
- Solution (only for matrices): \[\Sigma = \underset{y \in \mathcal{Y}}{\mathbb{E}}\left[yy^T\right] - \mathbb{E}[y]\mathbb{E}[y]^T\]
- LORD (Kaushal,2023)
- Our contributions:
- Generalize to non-linear layers
- Linear algebra \(\rightarrow\) Feature Distillation
- Tunable compromise local vs. global optimization
- Local \(\rightarrow\) Flexible semi-global
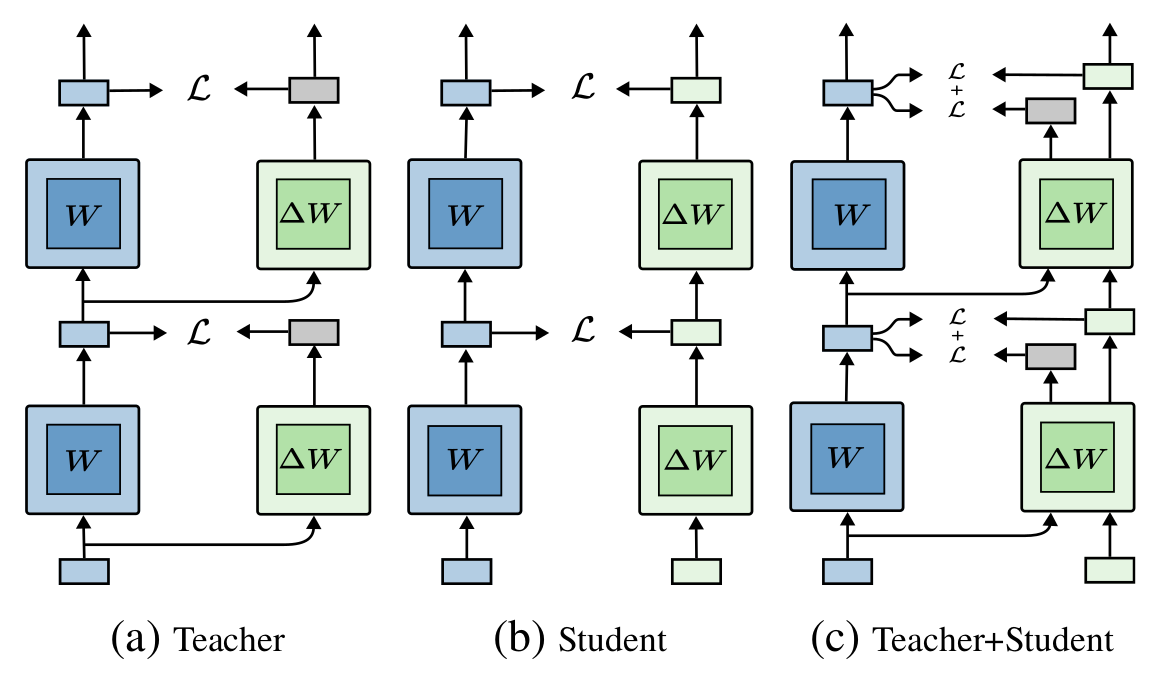
- Improved distillation
- Teacher-only \(\rightarrow\) Teacher & Student supervision
- Low-cost algo: bottom-first compression
- Generalize to non-linear layers
- Contribution: Better teacher/student inputs compromise
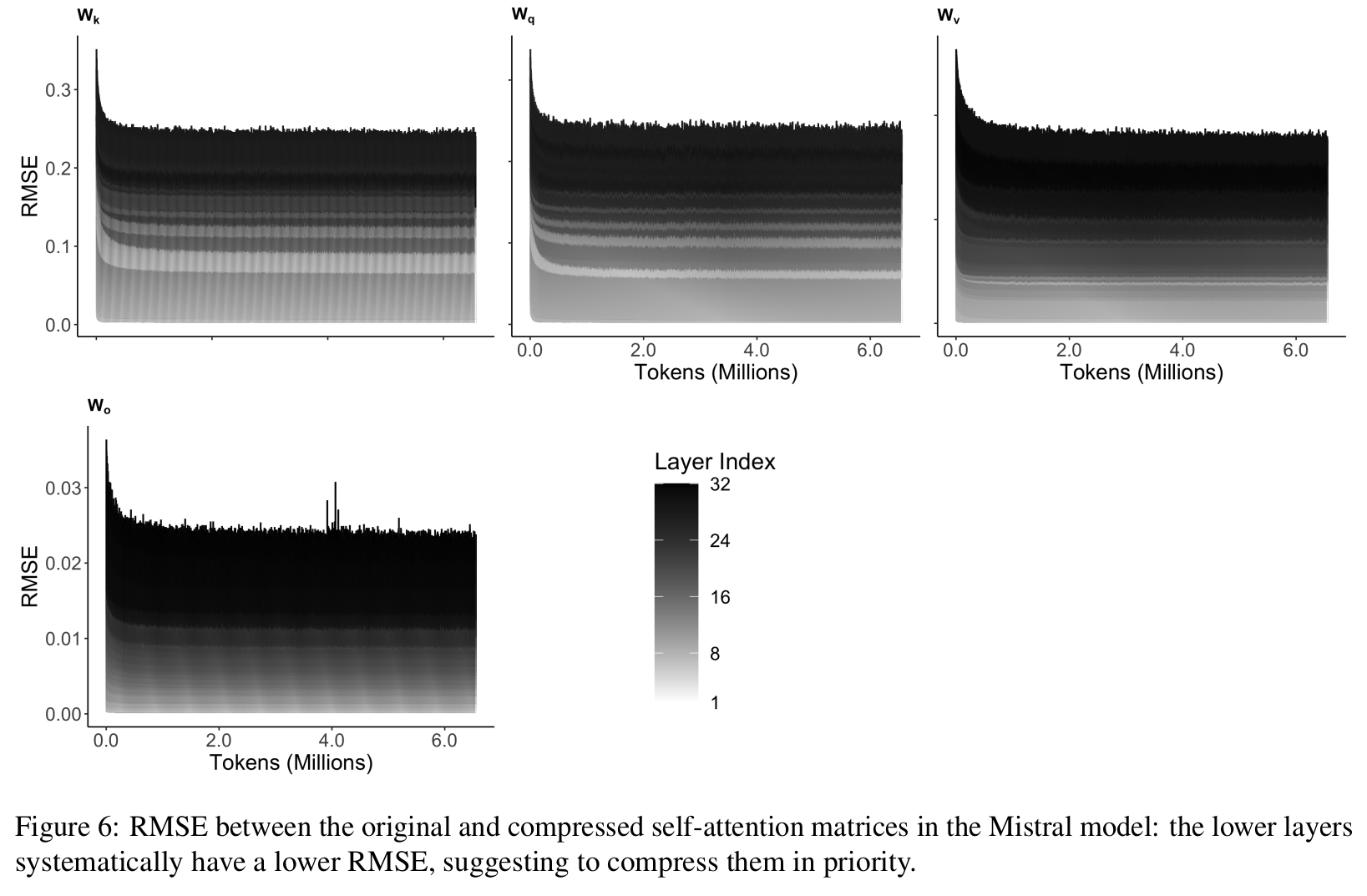
- Evidence: deeper layers are more robust to compression:
- Bottom-first compression:
- Low memory requirements:
- Compress layers 1 by 1
- No backprop
- Low computational cost & sample-efficient:
- Partial forward pass
- SVD init: reduce data reqs
- Low memory requirements:
Work published at NAACL’25
Results
- Compress Mixtral-48B, Gemma-27B on 1xA100
- Good results with Phi3-14B, Phi2-3B, Mistral-7B
- Mixtral-48b can run on 1xA100 with 2048-context & batch=4
- Compress Mamba-3B, FalconMamba-7B, Whisper-med
Future works: updating LLMs
- Continual learning too costly
- Every information must be seen 1000x during training
- Forgetting increases linearly \(\rightarrow\) rehearsal
- Investigating gradients-free knowledge editing

Thank you !
cerisara@loria.fr
Sources of all figures
- scaling test time: https://openai.com/index/learning-to-reason-with-llms/ (scalingtest.png)
- Kaplan’s training scaling laws: https://arxiv.org/pdf/2001.08361 (scale2.png)
- scaling law ICL: https://arxiv.org/html/2501.00070v1 (scalingicl.png)
- quantization effect on scaling laws: https://arxiv.org/html/2411.04330v1 (quantlimits.png)
- Sheared LLama: https://arxiv.org/pdf/2310.06694 (shearedllama.png)
- low rank weights: https://www.alignmentforum.org/posts/PDLfpRwSynu73mxGw/basic-facts-about-language-model-internals-1 (wrank1.png)
- forgetting when finetuning: https://openreview.net/pdf?id=0BMg0OgNTP (forgetting.png)
- All other figures are from our team