Low-rank compression of LLM

Christophe Cerisara

CNRS, LORIA, Synalp team

LLM brief overview

LLM: post-Machine Learning area?

• Limitations of ML approaches:
  • Only understand vector inputs
  • Unable to learn from 2 examples
• LLMs solve these limitations:
  • Understand English
  • Thanks to “reasoning”, can learn from 2 examples

Ex: last letter concatenation

(from Denny Zhou, Google)

Elon Musk	nk
Bill Gates	ls

• Obvious for humans with 2 examples
• ML approach:
  • enc-dec trained on tons of labeled data

• Qwen2.5-7b:

Perform last letter concatenation, as shown in these two examples. Words: Elon Musk Answer: nk Words: Bill Gates Answer: ls Words: Barack Obama Answer:

[…] So, the concatenation would be ka

• Requires more advanced prompting strategies with older models: CoT, analogical prompting…

Keys to success

• GPU
• Data
• Transformer
  • No data flow bottleneck

2017: the transformer

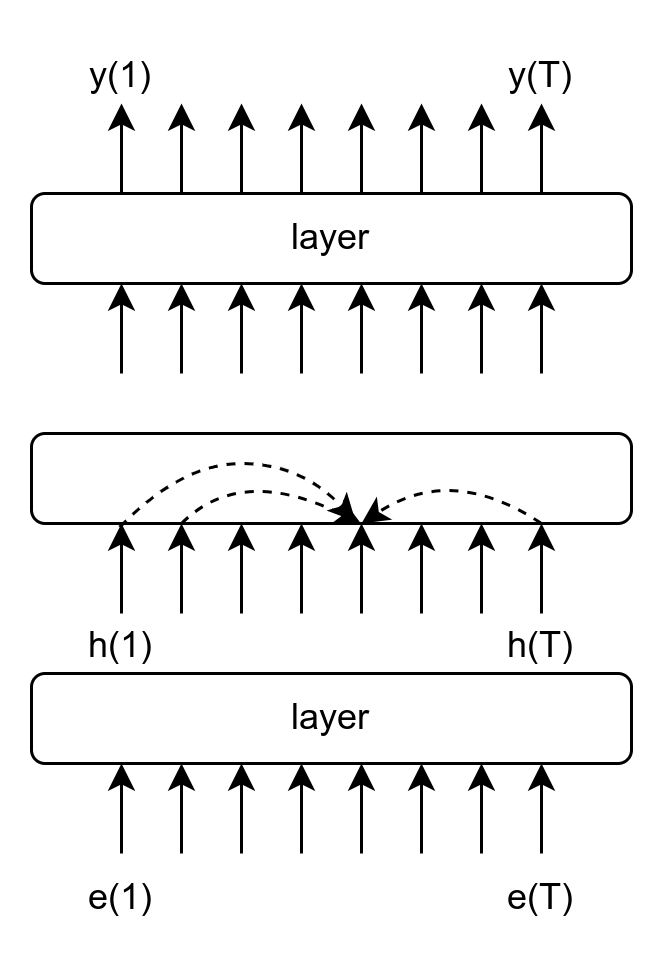
• Reason over layer steps
• Semi-Turing machine
• Learns to learn (2nd order-GD, TD)
• Reason over time steps

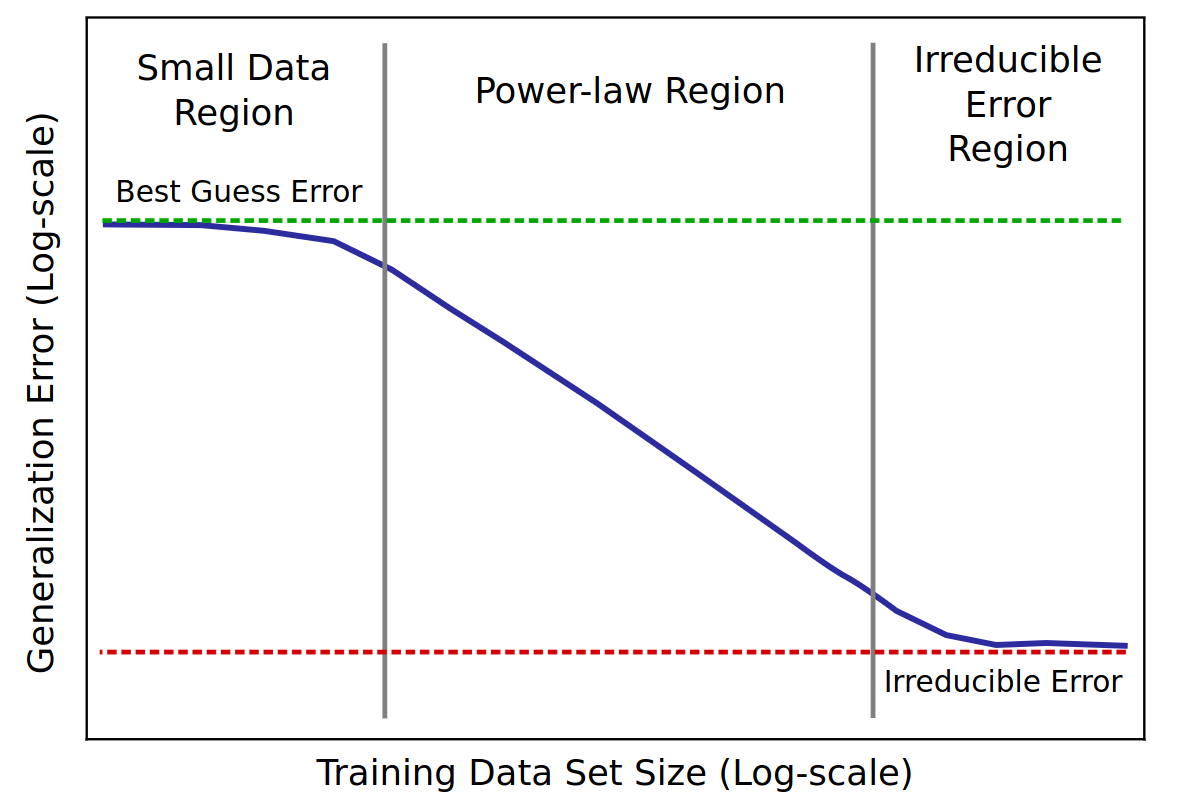
Transformer scaling laws

• The more data you train on
  • the more the LLM knows about
  • the better the LLM generalizes
• scaling law = power law = \(y(x) = ax^{-\gamma} +b\)
• \(y(x) =\) test loss
• \(\gamma\) = slope

Baidu paper 2017

Chinchilla scaling law 2022

\(L=\) pretraining loss

Google 2022: paper1, paper2 Flops, Upstream (pretraining), Downstream (acc on 17 tasks), Params

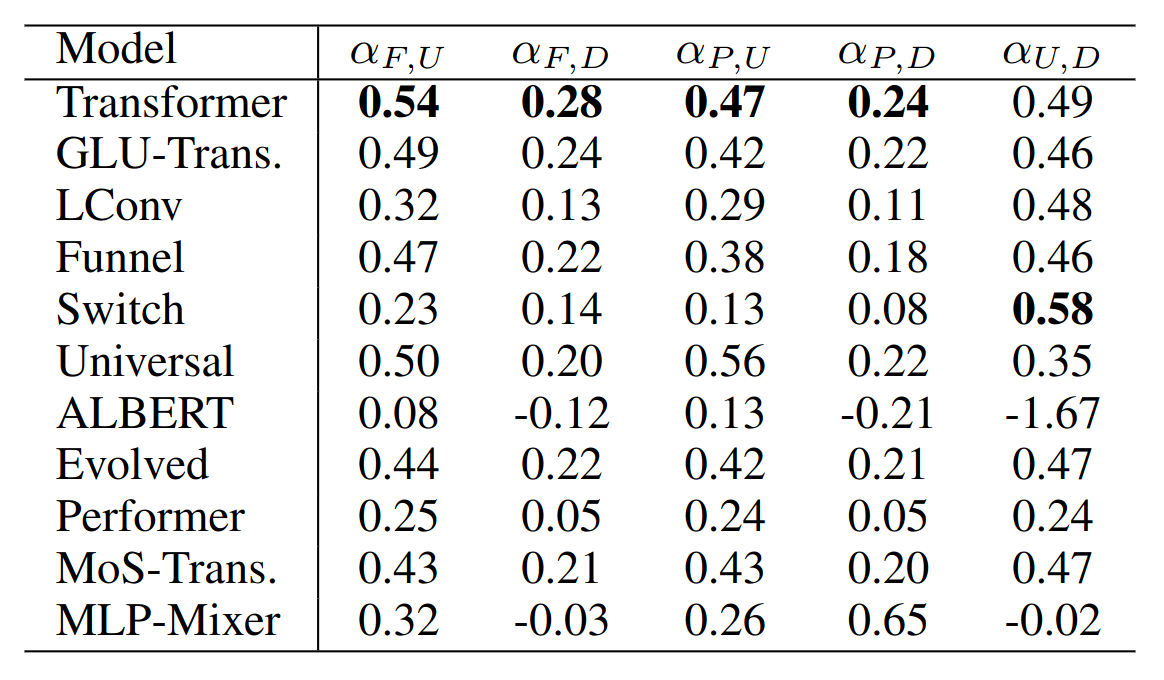
Scaling laws and pruning

• Recent models are not Chinchilla-optimal
• SmolLMs improve accessibility
• Quantization impacts scaling laws

“Scaling Laws for Precision” (Nov, 2024)

LLM pruning

• Reducing LLM size and cost:
  • Quantization
  • Distillation
  • Pruning
  • Low-rank compression

Motivations

• In many target applications, a lot of knowledge is not required
• May information stored in LLMs be sparse?
  • Despite the fact that LLMs are trained on >10T words…

• Lottery Ticket Hypothesis:
  • Each neural network contains a sub-network (winning ticket) that, if trained again in isolation, matches the performance of the full model.

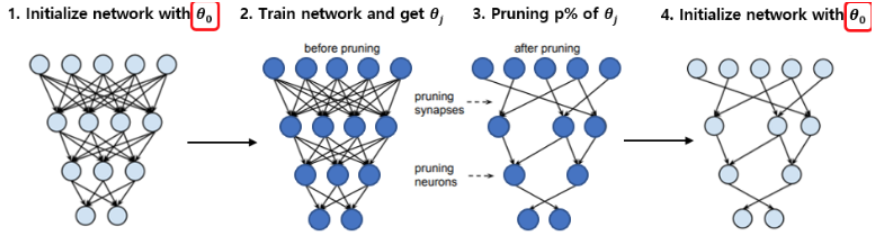
• Advantages:
  • Can remove 90% parameters nearly without loss in performances (on image tasks)
• Drawbacks:
  • Impossible to find the winning mask without training first the large model

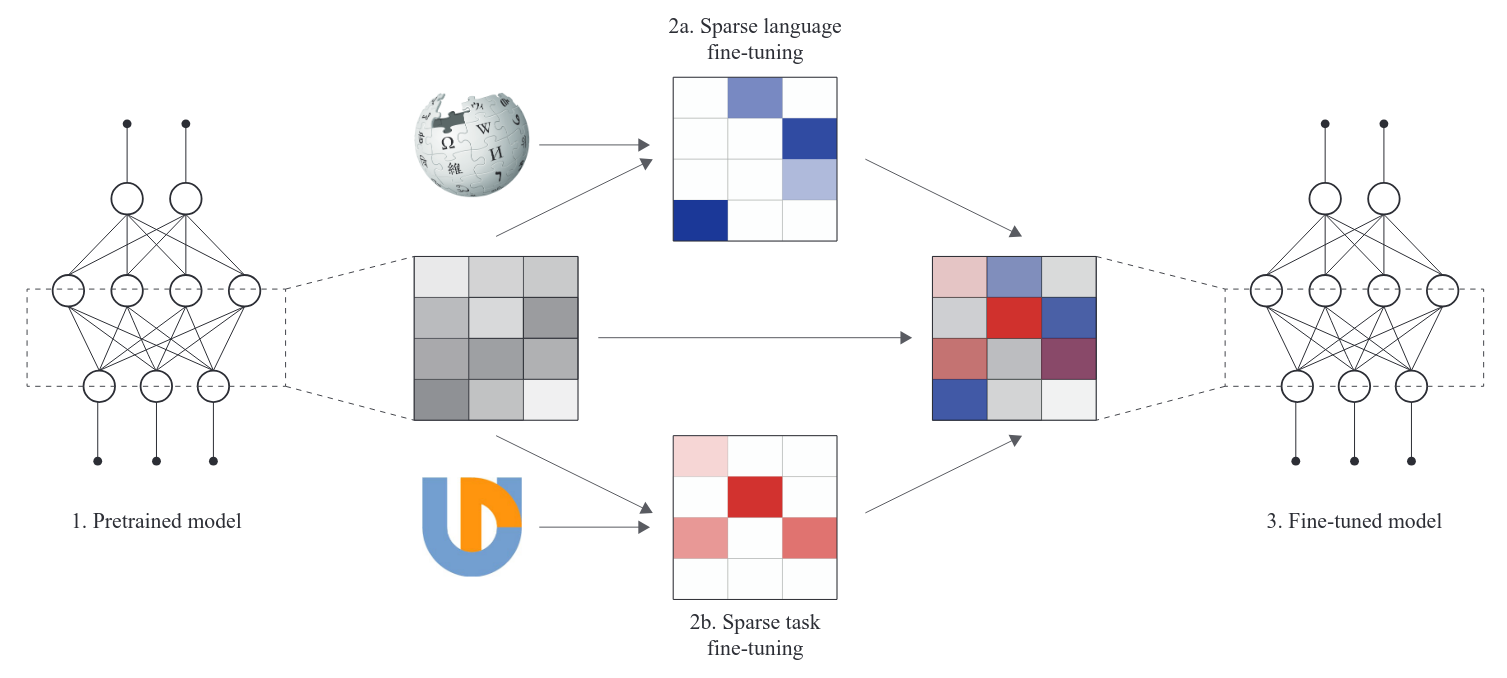
• can be applied to sparse FT

• FT an LLM on specific task/lang

• extract the mask = params that change most

• rewind the LLM and re-FT with mask

• sparse finetunes can be combined without overlapping!

• Low-rank approaches with LLMs:
  • LoRA: finetune within a lower dimensional space
  • GaLore: gradients low-rank projection
  • LORD: low-rank decomposition of weight matrices
  • CALDERA: joint quantization & low-rank projection
  • …

Pruning generic LLMs

• Can we prune a pretrained generic LLM so that it’s still generic?
• Is there “room” for pruning, given all the knowledge the LLM has memorized?
• \(\rightarrow\) Study the rank of parameters

Low-rank matrices

• Weight matrices in LLMs are “slightly low-rank”, or “not totally full-rank”

• Activations are low-rank!

• Approximations of activations: \[\widehat{\Delta W} = \underset{{\Delta W}}{\mathrm{argmin}} \;\; \frac{1}{N}\sum\limits_{x \in \mathcal{D}}\|Wx - {\Delta Wx}\|_{F}\]
• Optimal solution: PCA of covariance: \[\Sigma = \underset{y \in \mathcal{Y}}{\mathbb{E}}\left[yy^T\right] - \mathbb{E}[y]\mathbb{E}[y]^T\]
• Used for LSTM & BERT in (Chen,2021), for transformers in (Yu,2023), and see LORD in (Kaushal,2023)

• Limitations of activations approx:
  • Only linear layers
  • Only “Teacher” distillation (aka Atomic feature distillation in (Yu,2023))
  • Only local distillation

–

Next: work of Yaya Sy, Ph.D. student in Synalp

• Proposal 1: Generalize to non-linear layers:
  • The minimization objective can be viewed as Feature Distillation
  • Replace SVD with gradient descent
  • Teacher module \(\mathcal{T}^{(i)}(X; \Theta^{(i)})\) and Student module \(\mathcal{S}^{(i)}(X; \Delta \Theta^{(i)})\)

\[\widehat{\Delta \Theta^{(i)}} = \underset{{\Delta \Theta^{(i)}}}{\mathrm{argmin}} \;\; \mathcal{L}^{(i)}(Y^{(i)}, \; \widehat{Y}^{(i)})\]

• Because of unstabilities, augment L1 loss as (Chang,2022):

\[\mathcal{L}^{(i)} = \sum_{t=1}^{b} \left[ \frac{1}{D} \left\| Y^{(i)}_{t} - \widehat{Y}^{(i)}_{t} \right\|_1 - \log \sigma \left( \cos \left( Y^{(i)}_{t}, \widehat{Y}^{(i)}_{t} \right) \right) \right]\]

• Trained with SGD
• Converges towards SVD solution in the linear case

• Proposal 2: Better teacher/student inputs compromise

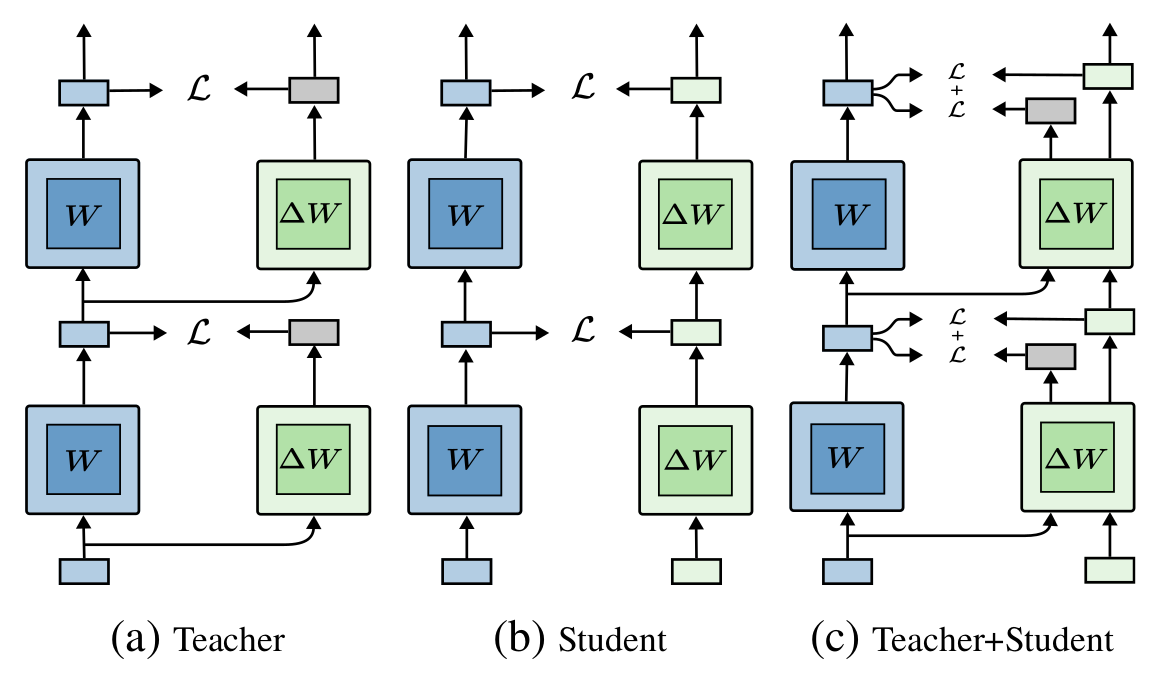
• Teacher-only: fast convergence, but mismatch btw train/test
• Student-only: no mismatch, but slow convergence due to errors propagation
• Teacher+Student: best compromise

• Proposal 3: Module-level distillation
  • Support of non-linear layers \(\rightarrow\) any stack of layers
  • Better compromise between atomic/local distillation (matrix level) and global distillation (transformer level)
  • We experiments at layer-level

• Every layer has the same rank?

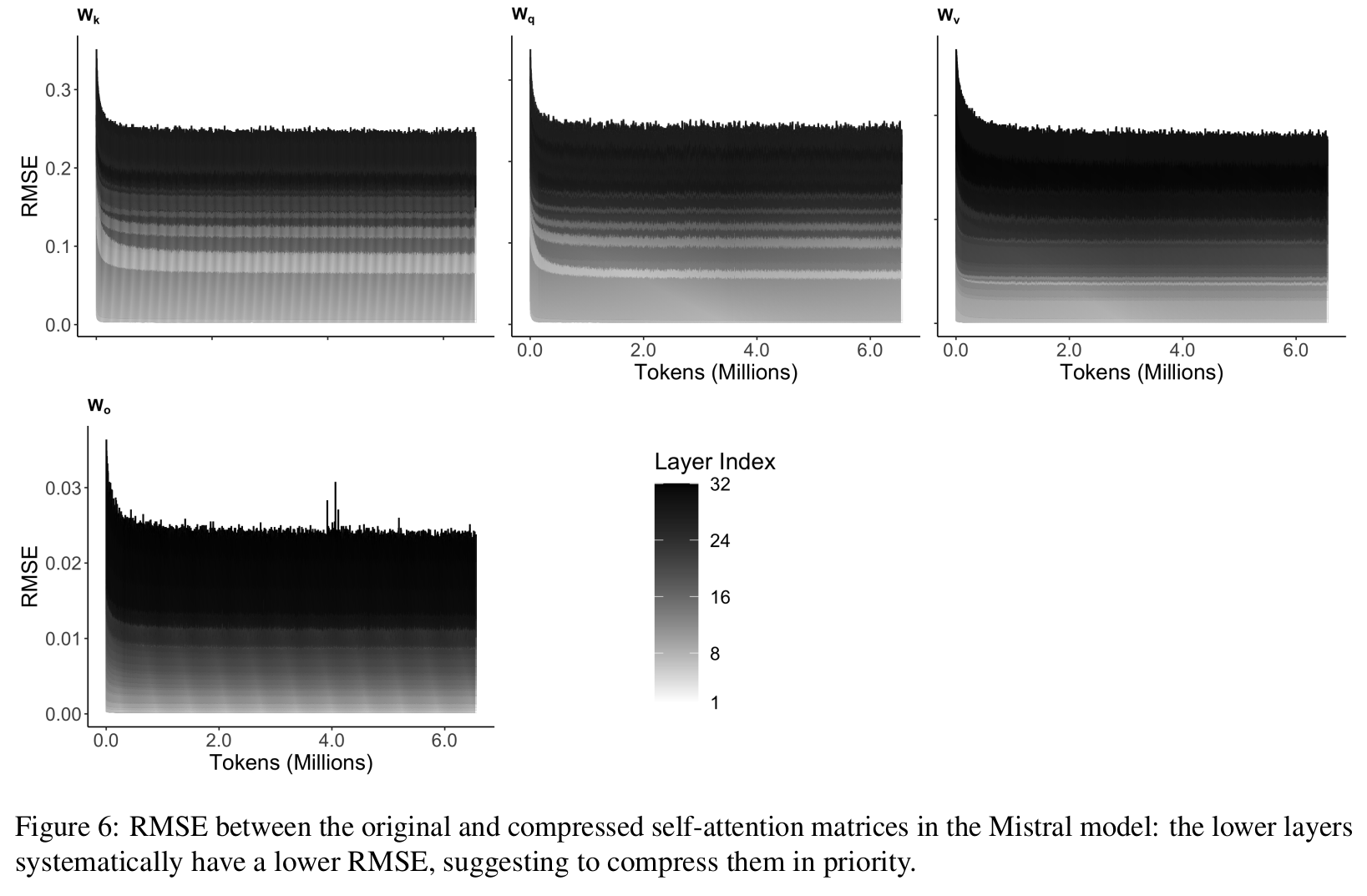
• Bottom-first compression:
  • Low-memory reqs:
    • process 1 layer at a time
    • no backprop from top needed
  • Low-cost:
    • partial forward pass
    • initialize with SVD: few calibration data needed

Results

• Compress Mixtral-48B, Gemma-27B on only 1xA100
• Good results with Phi3-14B, Phi2-3B, Mistral-7B
• Mixtral-48b now fits with 2048-context & batch=4 on a single A100!
• Compress Mamba-3B, FalconMamba-7B, Whisper-med

Conclusion

• Low-rank is everywhere in LLM tools
• But it’s not enough to make LLMs commodities:
  • Quantization is more efficient
  • Hardware/software optimization is key!

Happy to chat! cerisara@loria.fr, @cerisara@mastodon.online